Dans le cas d'un vecteur aléatoire dont les composantes sont des variables
aléatoires associées à un même processus, l'ensemble des valeurs
d'autocorrélation ou de covariance peut être rassemblé dans une matrice de
corrélation ou de covariance. Un vecteur à k composantes 
engendre une matrice 
à
éléments:
matrice de corrélation: 
où le symbole 
désigne l'opérateur transposé d'un vecteur.
matrice de covariance: 
Si le vecteur résulte de l'échantillonnage régulier d'un processus
stationnaire, les valeurs de corrélation ou de covariance ne dépendent plus que
de la différence 
où
est
le pas d'échantillonnage. De plus, on a 
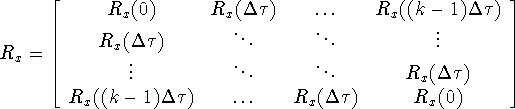
Une telle matrice est symétrique et chaque diagonale est composée d'éléments identiques (matrice de Toepliz).
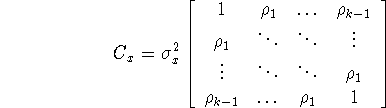
où 
.
Ces deux matrices s'identifient dans le cas de processus à moyenne nulle. On
montre facilement qu'une matrice de covariance est une matrice symétrique
définie positive ( 
).
Un cas particulier intéressant intervient lorsque les échantillons sont non
corrélés: ceci entraine l'annulation des coefficients de corrélation 
et
la matrice de covariance se réduit alors à une matrice diagonale d'éléments 
.
Transformation linéaire: Si l'on effectue un changement de variable
linéaire de la forme Y = AX où A est une matrice quelconque
de constantes (pas forcément carrée), alors on a les résultats suivants:
E(Y) = A E(X) et 
.
Normalisation d'un vecteur aléatoire: On appelle transformation de
Mahalanobis, la transformation 
. Le vecteur Y est un vecteur centré réduit à composantes non
corrélées.
Distance de Mahalanobis: On appelle distance de Mahalanobis de
X à la quantité 
:
.
Cette distance permet de mesurer la distance d'une réalisation d'un vecteur
aléatoire à un échantillon caractérisé par sa position (vecteur moyenne) et sa
dispersion (matrice de covaraince).
Jean-Michel JOLION